The work function of sodium metal is $4.41 \times 10^{-19} \mathrm{~J}$. If photons of wavelength $300 \mathrm{~nm}$ are incident on the metal, the kinetic energy of the ejected electrons will be $\left(h=6.63 \times 10^{-34} \mathrm{~J} \mathrm{~s} ; c=3 \times 10^{8} \mathrm{~m} / \mathrm{s}\right)$
(222)
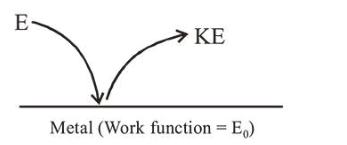
$\mathrm{E}=\mathrm{E}_{0}+(\mathrm{KE})_{\max }$
$\frac{h c}{\lambda}=4.41 \times 10^{-19}+\mathrm{KE}$
$\frac{6.63 \times 10^{-34} \times 3 \times 10^{8}}{300 \times 10^{-9}}=4.41 \times 10^{-19}+\mathrm{KE}$
So, $(\mathrm{KE})_{\max }=6.63 \times 10^{-19}-4.41 \times 10^{-19}$
$=2.22 \times 10^{-19} \mathrm{~J}=222 \times 10^{-21} \mathrm{~J}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.