Question:
The vertical height of a conical tent is 42 dm and the diameter of its base is 5.4 m. Find the number of persons it can accommodate if each person is to be allowed 29.16 cubic dm.
Solution:
Radius of conicaltent, $r=\frac{5.4}{2}$
$=2.7 \mathrm{~m}$
$=27 \mathrm{dm}$
Height of conical tent h = 42 dm
The volume of conical tent
$=\frac{1}{3} \pi r^{2} h$
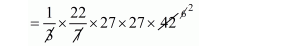
$=22 \times 27 \times 27 \times 2$
$=32076 \mathrm{dm}^{3}$
Since, each person is to be allowed $29.16 \mathrm{dm}^{3}$,
Therefore,
$=\frac{\text { volume of conical tent }}{\text { place to be allow to each person }}$
$=\frac{32076}{29.16}$
$=\frac{3207600}{2916}$
No. of person $=1100$
