The value of the determinant

Let $\Delta=\left|\begin{array}{ccc}\cos (x+y) & -\sin (x+y) & \cos 2 y \\ \sin x & \cos x & \sin y \\ -\cos x & \sin x & \sin y\end{array}\right|$

$\Delta=\left|\begin{array}{ccc}\cos (x+y) & -\sin (x+y) & \cos 2 y \\ \sin x & \cos x & \sin y \\ -\cos x & \sin x & \sin y\end{array}\right|$

Applying $R_{2} \rightarrow \sin y R_{2}$ and $R_{3} \rightarrow \cos y R_{3}$

$=\frac{1}{\sin y \cos y}\left|\begin{array}{ccc}\cos (x+y) & -\sin (x+y) & \cos 2 y \\ \sin x \sin y & \cos x \sin y & \sin ^{2} y \\ -\cos x \cos y & \sin x \cos y & \sin y \cos y\end{array}\right|$

Applying $R_{1} \rightarrow R_{1}+R_{2}+R_{3}$

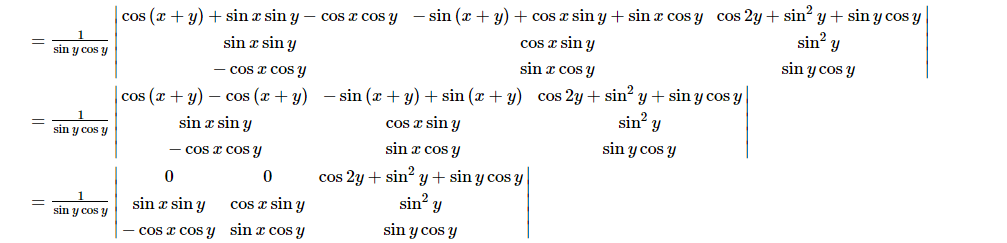
Expanding through $R_{1}$

$=\frac{1}{\sin y \cos y}\left[\left(\cos 2 y+\sin ^{2} y+\sin y \cos y\right)\left(\sin ^{2} x \sin y \cos y+\cos ^{2} x \sin y \cos y\right)\right]$

$=\frac{1}{\sin y \cos y}\left[\left(\cos 2 y+\sin ^{2} y+\sin y \cos y\right) \sin y \cos y\left(\sin ^{2} x+\cos ^{2} x\right)\right]$

$=\left[\left(\cos 2 y+\sin ^{2} y+\sin y \cos y\right)\left(\sin ^{2} x+\cos ^{2} x\right)\right]$

$=\left[\left(\cos 2 y+\sin ^{2} y+\sin y \cos y\right)(1)\right]$

$=\left(\cos 2 y+\sin ^{2} y+\sin y \cos y\right)$

$=\left(1-2 \sin ^{2} y+\sin ^{2} y+\sin y \cos y\right)$

$=\left(1-\sin ^{2} y+\sin y \cos y\right)$

Hence, the value of the determinant $\left|\begin{array}{ccc}\cos (x+y) & -\sin (x+y) & \cos 2 y \\ \sin x & \cos x & \sin y \\ -\cos x & \sin x & \sin y\end{array}\right|$ depends on $y$ only.