The value of p for which the polynomial

Solution:

Here the given polynomial is $x^{3}+4 x^{2}-p x+8$

We have to find the value of p such that the polynomial is exactly divisible by 

First we have to write equation in basic format of divisibility like this

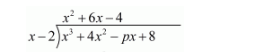
$x^{3}-2 x^{2}$

$6 x^{2}-p x+8$

$6 x^{2}-12 x$

$12 x-p x+8$

$\frac{4 x+8}{16 x-p x}$

After solving, we have seeing here the reminder is = 16x − px

So, to find the value of p we put the reminder is equal to zero.

Therefore

$16 x-p x=0$

$\Rightarrow \quad 16 x=p x$

$\Rightarrow \quad p=16$