The triangle of maximum area that can be inscribed in a given circle of

Triangle of maximum area that can be inscribed in a circle is an equilateral triangle. Let $\triangle \mathrm{ABC}$ be inscribed in circle,

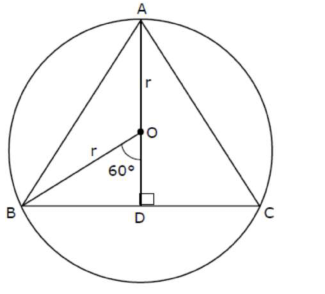
Now, in $\triangle O B D O D=r \cos 60^{\circ}=\frac{r}{2}$

Height $=A D=\frac{3 r}{2}$

Again in $\triangle \mathrm{ABD}$ Now $\sin 60^{\circ}=\frac{3 \frac{r}{2}}{A B}$

$\Rightarrow A B=\sqrt{3} r$