Question:
The thickness at the centre of a plano convex lens is $3 \mathrm{~mm}$ and the diameter is $6 \mathrm{~cm}$. If the speed of light in the material of the lens is $2 \times 10^{8} \mathrm{~ms}^{-1}$. The focal length of the lens is _______.
Correct Option: , 4
Solution:
$R^{2}=r^{2}+(R-t)^{2}$
$R^{2}=r^{2}+R^{2}+t^{2}-2 R t$
Neglecting $t^{2}$, we get
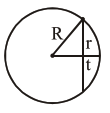
$R=\frac{r^{2}}{2 t}$
$\therefore \frac{1}{f}=(\mu-1)\left(\frac{1}{R}-\frac{1}{\infty}\right)=\frac{\mu-1}{R}$
$f=\frac{R}{\mu-1}=\frac{r^{2}}{2 t(\mu-1)}=\frac{\left(3 \times 10^{-2}\right)^{2}}{2 \times 3 \times 10^{-3} \times\left(\frac{3}{2}-1\right)}$
$=\frac{9 \times 10^{-4}}{6 \times 10^{-3} \times 1} \times 2$
$f=0.3 \mathrm{~m}=30 \mathrm{~cm}$
