The temperature of equal masses of three different liquids $\mathrm{x}, \mathrm{y}$ and $\mathrm{z}$ are $10^{\circ} \mathrm{C}, 20^{\circ} \mathrm{C}$ and $30^{\circ} \mathrm{C}$ respectively. The temperature of mixture when $x$ is mixed with $y$ is $16^{\circ} \mathrm{C}$ and that when $\mathrm{y}$ is mixed with $\mathrm{z}$ is $26^{\circ} \mathrm{C}$. The temperature of mixture when $\mathrm{x}$ and $\mathrm{z}$ are mixed will be :
Correct Option: , 3
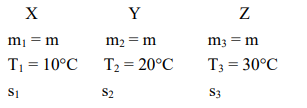
when $\mathrm{x} \& \mathrm{y}$ are mixed, $\mathrm{T}_{\mathrm{f}_{1}}=16^{\circ} \mathrm{C}$
$\mathrm{m}_{1} \mathrm{~s}_{1} \mathrm{~T}+\mathrm{m}_{2} \mathrm{~s}_{2} \mathrm{~T}_{2}=\left(\mathrm{m}_{1} \mathrm{~s}_{1}+\mathrm{m}_{2} \mathrm{~s}_{2}\right) \mathrm{Tf}_{1}$
$\mathrm{s}_{1} \times 10+\mathrm{s}_{2} \times 20=\left(\mathrm{s}_{1}+\mathrm{s}_{2}\right) \times 16$
$\mathrm{s}_{1}=\frac{2}{3} \mathrm{~s}_{2} \quad \ldots .$ (i)
when $\mathrm{y} \& \mathrm{z}$ are mixex, $\mathrm{T}_{\mathrm{f}_{2}}=26^{\circ} \mathrm{C}$
$\mathrm{m}_{2} \mathrm{~s}_{2} \mathrm{~T}+\mathrm{m}_{3} \mathrm{~s}_{3} \mathrm{~T}_{3}=\left(\mathrm{m}_{3} \mathrm{~s}_{3}+\mathrm{m}_{3} \mathrm{~s}_{3}\right) \mathrm{Tf} \mathrm{f}_{2}$
$\mathrm{s}_{2} \times 20+\mathrm{s}_{3} \times 30=\left(\mathrm{s}_{2}+\mathrm{s}_{3}\right) \times 26$
$\mathrm{s}_{3}=\frac{3}{2} \mathrm{~s}_{2}$ ............(II)
when $\mathrm{x} \& \mathrm{z}$ are mixex
$\mathrm{m}_{1} \mathrm{~s}_{1} \mathrm{~T}_{1}+\mathrm{m}_{3} \mathrm{~s}_{3} \mathrm{~T}_{3}=\left(\mathrm{m}_{1} \mathrm{~s}_{1}+\mathrm{m}_{3} \mathrm{~s}_{3}\right) \mathrm{Tf}$
$\frac{2}{3} s_{2} \times 10+\frac{2}{3} s_{2} \times 20=\left(\frac{2}{3} s_{2}+\frac{3}{2} s_{2}\right) T_{f}$
$\mathrm{T}_{\mathrm{f}}=23.84^{\circ} \mathrm{C}$
$\operatorname{Ans}(3)$
