Question:
The temperature $\theta$ at the junction of two insulating sheets, having thermal resistances $\mathrm{R}_{1}$ and $R_{2}$ as well as top and bottom temperatures $\theta_{1}$ and $\theta_{2}$ (as shown in figure) is given by :
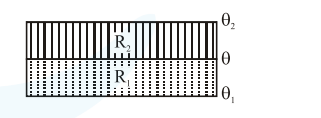
Correct Option: , 3
Solution:
Heat flow rate will be same through both
$\therefore \frac{\theta_{1}-\theta}{\mathrm{R}_{1}}=\frac{\theta-\theta_{2}}{\mathrm{R}_{2}}$
$\mathrm{R}_{2} \theta_{1}-\mathrm{R}_{2} \theta=\mathrm{R}_{1} \theta-\mathrm{R}_{1} \theta_{2}$
$\theta=\frac{R_{2} \theta_{1}+R_{1} \theta_{2}}{R_{1}+R_{2}}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.