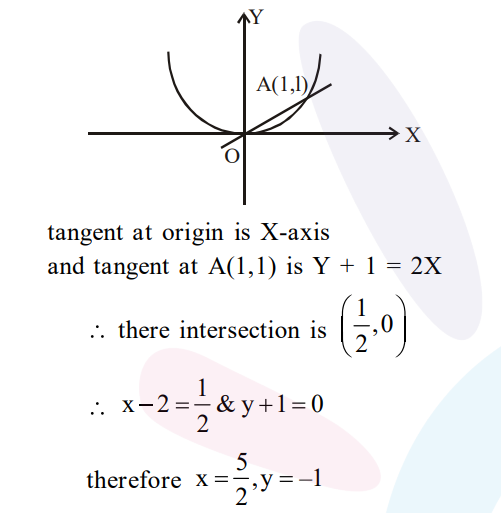Question:
The tangents to the curve $y=(x-2)^{2}-1$ at its points of intersection with the line $x-y=3$, intersect at the point :
Correct Option: , 3
Solution:
Put $\mathrm{x}-2=\mathrm{X} \& \mathrm{y}+1=\mathrm{Y}$
$\therefore$ given curve becomes $\mathrm{Y}=\mathrm{X}^{2}$ and $\mathrm{Y}=\mathrm{X}$