The sum of two numbers is 8 and 15 times the sum of their reciprocals is also 8.

Solution:

Let first numbers be $x$ and other $(8-x)$

Then according to question

$\left\{\frac{1}{x}+\frac{1}{(8-x)}\right\} \times 15=8$

$\left\{\frac{8-\not x+\not x}{x(8-x)}\right\}=\frac{8}{15}$

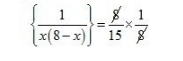
$x(8-x)=15$

$x^{2}-8 x+15=0$

$x^{2}-5 x-3 x+15=0$

$x(x-5)-3(x-5)=0$

$(x-5)(x-3)=0$

$x=5$

Or

$(x-3)=0$

$x=3$

Thus, two consecutive number be 3,5