The students of a class are made to stand in rows.

Let the number of students be $x$ and the number of row be $y$.then,

Number of students in each row $=\frac{x}{y}$

Where three students is extra in each row, there are one row less that is when each row has $\left(\frac{x}{y}+3\right)$ students the number of rows is $(y-1)$

Total number of students =no. of rowsno. of students in each row

$x=\left(\frac{x}{y}+3\right)(y-1)$

$x=\left(x+3 y-\frac{x}{y}-3\right)$

$0=\frac{-x}{y}+x-x+3 y-3$

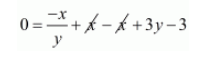
$0=\frac{-x}{y}+3 y-3$

If three students are less in each row then there are 2 rows more that is when each row has $\left(\frac{x}{y}-3\right)(y+2)$

Therefore, total number of students=Number of rowsNumber of students in each row

$x=\left(\frac{x}{y}-3\right)(y+2)$

$x=x-3 y+\frac{2 y}{x}-6$

$0=\frac{2 x}{y}+x-x-3 y-6$

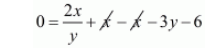
$0=\frac{2 x}{y}-3 y-6 \cdots(i i)$

Putting $\frac{x}{y}=u$ in $(i)$ and $(i i)$ equation we get

$-u+3 y-3=0 \cdots(i i i)$

$2 u-3 y-6=0 \cdots(i v)$

Adding $(i i i)$ and $(i v)$ equation we get

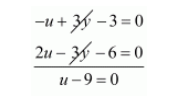
$u=9$

Putting $u=9$ in equation (iii) we get

$-u+3 y-3=0$

$-9+3 y-3=0$

$+3 y-12=0$

$3 y=12$

$y=\frac{12}{3}$

$y=4$

$u=9$

$\frac{x}{y}=9$

$\frac{x}{4}=9$

$x=9 \times 4$

$x=36$

Hence, the number of students in the class is 36.