Question:
The stream of a river is flowing with a speed of $2 \mathrm{~km} / \mathrm{h}$. A swimmer can swim at a speed of $4 \mathrm{~km} / \mathrm{h}$. What should be the direction of the swimmer with respect to the flow of the river to cross the river straight?
Correct Option: , 3
Solution:
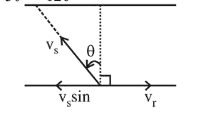
(3) To cross the river straight
$\mathrm{V}_{\mathrm{s}} \sin \theta=\mathrm{V}_{\mathrm{r}} \therefore \sin \theta=\frac{v_{r}}{v_{s}}=\frac{2}{4}=\frac{1}{2}$
$\therefore \theta=30^{\circ}$
Direction of swimmer with respect to flow
$=90^{\circ}+30^{\circ}=120^{\circ}$