Question:
The straight line $x+2 y=1$ meets the coordinate axes at A and B. A circle is drawn through A, $B$ and the origin. Then the sum of perpendicular distances from $A$ and $B$ on the tangent to the circle at the origin is :
Correct Option: , 2
Solution:
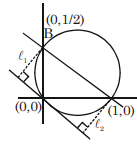
Equation of circle
$(x-1)(x-0)+(y-0)\left(y-\frac{1}{2}\right)=0$
$\Rightarrow x^{2}+y^{2}-x-\frac{y}{2}=0$
Equation of tangent of origin is $2 \mathrm{x}+\mathrm{y}=0$
$\ell_{1}+\ell_{2}=\frac{2}{\sqrt{5}}+\frac{1}{2 \sqrt{5}}$
$=\frac{4+1}{2 \sqrt{5}}=\frac{\sqrt{5}}{2}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.