Question:
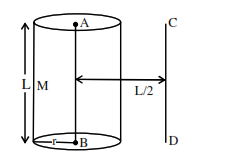
The solid cylinder of length $80 \mathrm{~cm}$ and mass $M$ has a radius of $20 \mathrm{~cm}$. Calculate the density of the material used if the moment of inertia of the cylinder about an axis CD parallel to $\mathrm{AB}$ as shown
in figure is $2.7 \mathrm{~kg} \mathrm{~m}^{2}$.
Correct Option: , 4
Solution:
Parallel axis theorem
$\mathrm{I}=\mathrm{I}_{\mathrm{CM}}+\mathrm{Md}^{2}$
$\mathrm{I}=\frac{\mathrm{Mr}^{2}}{2}+\mathrm{M}\left(\frac{\mathrm{L}}{2}\right)^{2}$
$2.7=\mathrm{M} \frac{(0.2)^{2}}{2}+\mathrm{M}\left(\frac{0.8}{2}\right)^{2}$
$2.7=M\left[\frac{2}{100}+\frac{16}{100}\right]$
$M=15 k g$
$\Rightarrow \rho=\frac{\mathrm{M}}{\pi \mathrm{r}^{2} \mathrm{~L}}=\frac{15}{\pi(0.2)^{2} \times 0.8}$
$=0.1492 \times 10^{3}$
Ans. 4
