The sides of a triangle are 35 cm,

Solution:

(c) Let $A B C$ be a triangle in which sides $A B=35 \mathrm{~cm}, B C=54 \mathrm{~cm}$ and $C A=61 \mathrm{~cm}$

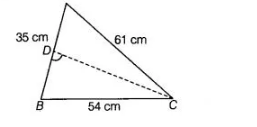
Now, semi-perimeter of a triangle,

$s=\frac{a+b+c}{2}=\frac{35+54+61}{2}=\frac{150}{2}=75 \mathrm{~cm}$

$\left[\because\right.$ semi-perimeter, $\left.s=\frac{a+b+c}{2}\right]$

$\because \quad$ Area of $\triangle A B C=\sqrt{s(s-a)(s-b)(s-c)}$ [by Heron's formula]

$=\sqrt{75(75-35)(75-54)(75-61)}$

$=\sqrt{75 \times 40 \times 21 \times 14}$

$=\sqrt{25 \times 3 \times 4 \times 2 \times 5 \times 7 \times 3 \times 7 \times 2}$

$=5 \times 2 \times 2 \times 3 \times 7 \sqrt{5}=420 \sqrt{5} \mathrm{~cm}^{2}$

Aso, Area of $\triangle A B C=\frac{1}{2} \times A B \times$ Altitude

$\Rightarrow \quad \frac{1}{2} \times 35 \times C D=420 \sqrt{5}$

$\Rightarrow \quad C D=\frac{420 \times 2 \sqrt{5}}{35}$

$\therefore \quad C D=24 \sqrt{5}$

Hence, the length of altitude is $24 \sqrt{5} \mathrm{~cm}$.