The side AB of a parallelogram ABCD is produced to any point P.

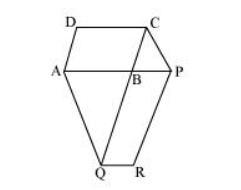
Solution:



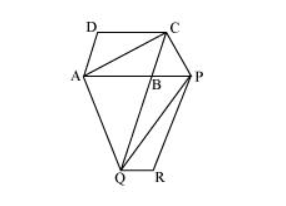
Let us join AC and PQ.

$\triangle A C Q$ and $\triangle A Q P$ are on the same base $A Q$ and between the same parallels $A Q$ and $C P$.

$\therefore$ Area $(\triangle A C Q)=$ Area $(\triangle A P Q)$

$\Rightarrow$ Area $(\triangle A C Q)-$ Area $(\triangle A B Q)=$ Area $(\triangle A P Q)-$ Area $(\triangle A B Q)$

$\Rightarrow$ Area $(\triangle A B C)=$ Area $(\triangle Q B P) \ldots(1)$

Since $A C$ and $P Q$ are diagonals of parallelograms $A B C D$ and $P B Q R$ respectively,

$\therefore$ Area $(\triangle A B C)=\frac{1}{2}$ Area $(A B C D) \ldots$(2)

Area $(\triangle \mathrm{QBP})=\frac{1}{2}$ Area $(\mathrm{PBQR})$...(3)

From equations $(1),(2)$, and $(3)$, we obtain

$\frac{1}{2}$ Area $(A B C D)=\frac{1}{2}$ Area $(P B Q R)$

Area $(A B C D)=$ Area $(P B Q R)$