The shortest distance between the

The shortest distance between line $y=x$ and parabola $=$ the distance $L M$ between line $y=x$ and tangent of parabola having slope 1 .

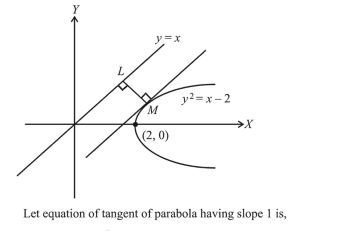
$y=m(x-2)+\frac{a}{m}$

Here $m=1$ and $a=\frac{1}{4}$

$\therefore$ equation of tangent is: $y=x-\frac{7}{4}$

Distance between the line $y-x=0$ and $y-x+\frac{7}{4}=0$

$=\left|\frac{\frac{7}{4}-0}{\sqrt{1^{2}+1^{2}}}\right|=\frac{7}{4 \sqrt{2}}$