The shadow of a tower, when the angle of elevation of the sun is 45°,

Let h be height of tower AB and angle of elevation are 45° and 60° are given.

In a triangle OAC, given that AB = 10+x and BC = x

Now we have to find height of tower.

So we use trigonometrical ratios.

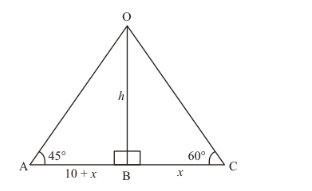
In a triangle OAB,

$\Rightarrow \quad \tan A=\frac{O B}{A B}$

$\Rightarrow \tan 45^{\circ}=\frac{O B}{A B}$

$\Rightarrow \quad 1=\frac{h}{10+x}$

$\Rightarrow \quad h=10+x$

Therefore $x=h-10$

Again in a triangle,

$\Rightarrow \quad \tan C=\frac{O B}{B C}$

$\Rightarrow \quad \tan 60^{\circ}=\frac{O B}{B C}$

$\Rightarrow \quad \sqrt{3}=\frac{h}{x}$

$\Rightarrow \quad h=\sqrt{3} x$

Put $x=h-10$

$\Rightarrow \quad h=\sqrt{3}(h-10)$

$\Rightarrow \quad h=\sqrt{3} h-10 \sqrt{3}$

$\Rightarrow \quad 10 \sqrt{3}=h(\sqrt{3}-1)$

$\Rightarrow \quad h=\frac{10 \sqrt{3}}{(\sqrt{3}-1)}$

$\Rightarrow \quad h=\frac{10 \times 1.732}{(1.732-1)}$

$\Rightarrow \quad h=\frac{17.32}{0.372}$

$\Rightarrow \quad h=23.66$

Hence height of tower is $23.66 \mathrm{~m}$.