The resultant of these forces $\overrightarrow{\mathrm{OP}}, \overrightarrow{\mathrm{OQ}}, \overrightarrow{\mathrm{OR}}, \overrightarrow{\mathrm{OS}}$ and $\overrightarrow{\mathrm{OT}}$ is approximately ...... $\mathrm{N}$.
[Take $\sqrt{3}=1.7, \sqrt{2}=1.4$ Given $\hat{\mathrm{i}}$ and $\hat{\mathrm{j}}$ unit vectors along $\mathrm{x}, \mathrm{y}$ axis]
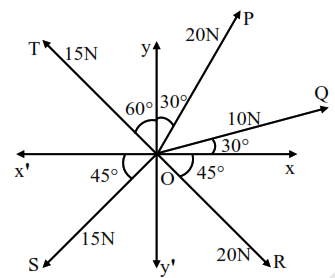
Correct Option: 1
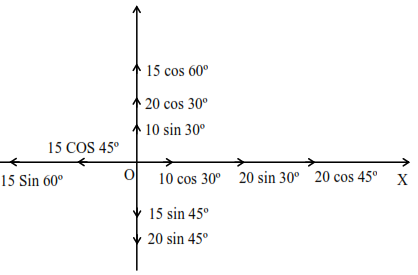
$\overrightarrow{\mathrm{F}}_{\mathrm{x}}=\left(10 \times \frac{\sqrt{3}}{2}+20\left(\frac{1}{2}\right)+20\left(\frac{1}{\sqrt{2}}\right)-15\left(\frac{1}{\sqrt{2}}\right)-15\left(\frac{\sqrt{3}}{2}\right)\right) \hat{\mathrm{i}}$$=9.25 \hat{\mathrm{i}}$
$\overrightarrow{\mathrm{F}}_{\mathrm{y}}=\left(15\left(\frac{1}{2}\right)+20\left(\frac{\sqrt{3}}{2}\right)+10\left(\frac{1}{2}\right)-15\left(\frac{1}{\sqrt{2}}\right)-20\left(\frac{1}{\sqrt{2}}\right)\right) \hat{\mathrm{j}}$$=5 \hat{\mathrm{j}}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.