Question:
The radius of the base of a right circular cone of semi-vertical angle $\alpha$ is $r$. Show that its volume is $\frac{1}{3} \pi r^{3} \cot \alpha$ and curved surface area is $\pi r^{2} \operatorname{cosec} \alpha$.
Solution:
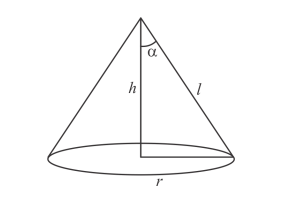
$\sin \alpha=\frac{r}{l}$
$\Rightarrow r \operatorname{cosec} \alpha=l$
$\tan \alpha=\frac{r}{h}$
$\Rightarrow r \cot \alpha=h$
Volume $=\frac{1}{3} \pi r^{2} h$
$=\frac{1}{3} \pi r^{2} \cdot r \cot \alpha$
$=\frac{1}{3} \pi r^{3} \cot \alpha$
Surface area $=\pi r l$
$=\pi r \cdot r \operatorname{cosec} \alpha$
$=\pi r^{2} \operatorname{cosec} \alpha .$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.