Question:
The radius of a circle with centre O is 7 cm. Two radii OA and OB are drawn at right angles to each other. Find the areas of minor and major
segments.
Solution:
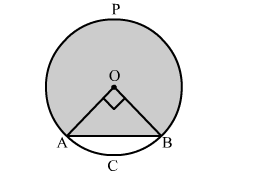
Area of minor segment = Area of sector AOBC − Area of right triangle AOB
$=\frac{90^{\circ}}{360^{\circ}} \pi(\mathrm{OA})^{2}-\frac{1}{2} \times \mathrm{OA} \times \mathrm{OB}$
$=\frac{1}{4} \times \frac{22}{7} \times(7)^{2}-\frac{1}{2} \times 7 \times 7$
$=\frac{1}{4} \times \frac{22}{7} \times(7)^{2}-\frac{1}{2} \times 7 \times 7$
$=38.5-24.5$
$=14 \mathrm{~cm}^{2}$
Area of major segment APB = Area of circle − Area of minor segment
$=\pi(\mathrm{OA})^{2}-14$
$=\frac{22}{7} \times(7)^{2}-14$
$=154-14$
$=140 \mathrm{~cm}^{2}$
Hence, the area of major segment is 140 cm2 .
