The radius of a circle is 30 cm.

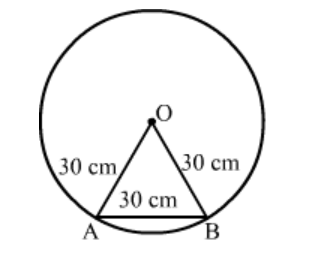
Let AB be the chord and O be the centre of the circle.

Here,

AO = BO = AB = 30 cm

Therefore, $\Delta A O B$ is an equilateral triangle.

Now,

Radius = 30 cm

$\theta=60^{\circ}=\left(60 \times \frac{\pi}{180}\right)=\frac{\pi}{3} \operatorname{radian}$

$\theta=\frac{\text { Arc }}{\text { Radius }}$

$\Rightarrow \frac{\pi}{3}=\frac{\operatorname{Arc}}{30}$

$\Rightarrow \operatorname{Arc}=\frac{30 \pi}{3}=10 \pi \mathrm{cm}$