The projectile motion of a particle of mass $5 \mathrm{~g}$ is shown in the figure.
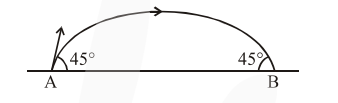
The initial velocity of the particle is
$5 \sqrt{2} \mathrm{~ms}^{-1}$ and the air resistance is assumed to be negligible. The magnitude of the change in momentum between the points $A$ and $B$ is
$x \times 10^{-2} \mathrm{kgms}^{-1}$. The value of $\mathrm{x}$, to the nearest integer, is_______.
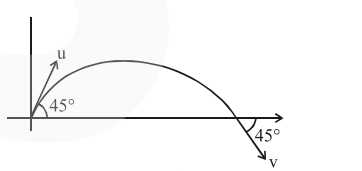
$|\overrightarrow{\mathrm{u}}|=|\overrightarrow{\mathrm{v}}|$ $\ldots(1)$
$\overrightarrow{\mathrm{u}}=u \cos 45 \hat{\mathrm{i}}+\mathrm{u} \sin 45 \hat{\mathrm{j}} \quad \ldots(2)$
$\vec{v}=v \cos 45 \hat{i}-v \sin 45 \hat{j}$ ......(3)
$|\overrightarrow{\Delta \mathrm{P}}|=|\mathrm{m}(\overrightarrow{\mathrm{v}}-\overrightarrow{\mathrm{u}})|$ .......(4)
$\Delta \mathrm{P}=2 \mathrm{mu} \sin 45^{\circ}$
$=2 \times 5 \times 10^{-3} \times 5 \sqrt{2} \times \frac{1}{\sqrt{2}}$
$=50 \times 10^{-3}$
$=5 \times 10^{-2}$
