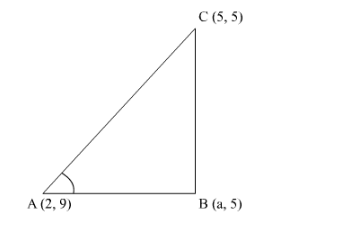
The points A (2, 9), B (a, 5), C (5, 5) are the vertices

It is given that ABC is a right angled triangle..Vertices of triangle are

A( 2,9 ), B( a,5 ), C( 5, 5 ).

We have to find the value of a and area of the triangle.

is a right angled triangle.

We know that length of a line with coordinates of end points $\left(x_{1}, y_{1}\right)$ and $\left(x_{2}, y_{2}\right)$

$=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}$

Hence in $\triangle A B C$

$A B=\sqrt{(a-2)^{2}+(5-9)^{2}}$

$=\sqrt{a^{2}-4 a+4+16}$

$=\sqrt{a^{2}-4 a+20}$.......(1)

$B C=\sqrt{(a-5)^{2}+(5-5)^{2}}$

$=\sqrt{a^{2}-10 a+25}$

$=\sqrt{a^{2}-10 a+25} \ldots \ldots(2)$

$A C=\sqrt{(5-2)^{2}+(5-9)^{2}}$

$=\sqrt{9+16}$

$=\sqrt{25}$

$=5$

Therefore, applying Pythagoras Theorem to right 

$A B^{2}+B C^{2}=A C^{2}$

$\left(\sqrt{a^{2}-4 a+20}\right)^{2}+\left(\sqrt{a^{2}-10 a+25}\right)^{2}=5^{2}$

$a^{2}-4 a+20-a^{2}-10 a+25=25$

$2 a^{2}-14 a+20=0$

$2\left(a^{2}-7 a+10\right)=0$

$a^{2}-7 a+10=0$

$a^{2}-5 a-2 a+10=0$

$a(a-5)+2(a-5)=0$

$(a-5)(a-2)=0$

$a=5,2$

$a \neq 5$ because it will make the coordinates of $B$ and $C$ same

Therefore $a=2$

Putting a = 2 in (1) and (2)

$A B=\sqrt{2^{2}-4 \times 2+20}$

$=\sqrt{16}$

$=4$

$B C=\sqrt{a^{2}-10 a+25}$

$=\sqrt{2^{2}-10 \times 2+25}$

$=\sqrt{9}$

$=3$

Area of right angled $\triangle A B C=\frac{1}{2} \times A B \times B C$

$=\frac{1}{2} \times 4 \times 3$

$=6$