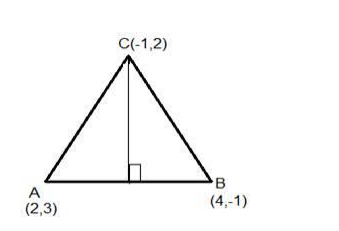
The points A(2, 3), B(4, -1) and C(-1, 2)

Given: points A(2, 3), B(4, -1) and C(-1, 2) are the vertices of ΔABC

To find : length of the perpendicular from C on AB and the area of ΔABC

Formula used:

We know that the length of the perpendicular from $(m, n)$ to the line $a x+b y+c=0$ is

$D=\frac{|a m+b n+c|}{\sqrt{a^{2}+b^{2}}}$

The equation of the line joining the points $\left(\mathrm{x}_{1}, \mathrm{y}_{1}\right)$ and $\left(\mathrm{x}_{2}, \mathrm{y}_{2}\right)$ is given by

$\frac{y-y_{1}}{y_{2}-y_{1}}=\frac{x-x_{1}}{x_{2}-x_{1}}$

The equation of the line joining the points $A(2,3)$ and $B(4,-1)$ is

Here $x_{1}=2 y_{1}=3$ and $x_{2}=4 y_{2}=-1$

$\frac{y-3}{x-2}=\frac{-1-3}{4-2}=\frac{-4}{2}=-2$

$y-3=-2 x+4$

$2 x+y-7=0$

The equation of the line is $2 x+y-7=0$

The length of perpendicular from $C(-1,2)$ to the line $A B$

The given equation of the line is $2 x+y-7=0$

Here $m=-1$ and $n=2, a=2, b=1, c=-7$

$D=\frac{|2(-1)+1(2)-7|}{\sqrt{2^{2}+1^{2}}}$

$D=\frac{-2+2-7}{\sqrt{4+1}}=\frac{|-7|}{\sqrt{5}}=\frac{|-7|}{\sqrt{5}}=\frac{7}{\sqrt{5}}$

$D=\frac{7}{\sqrt{5}}$

The length of the perpendicular from $C$ on $A B$ is $\frac{7}{\sqrt{5}}$ units.

Height of the triangle is $\frac{7}{\sqrt{5}}$ units

The distance between points $A\left(x_{1}, y_{1}\right)$ and $B\left(x_{2}, y_{2}\right)$ is given by

$A B=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}$

Here $x 1=2$ and $y 1=3, x 2=4$ and $y 2=-1$

$A B=\sqrt{(4-2)^{2}+(-1-3)^{2}}=\sqrt{2^{2}+(-4)^{2}}=\sqrt{4+16}=\sqrt{20}=2 \sqrt{5}$

Base $A B=2 \sqrt{5}$ units

Area of the triangle $=\frac{1}{2} \times \mathrm{BASE} \times \mathrm{HEIGHT}$

Area of the triangle $A B C=\frac{1}{2} \times A B \times H E I G H T=\frac{1}{2} \times 2 \sqrt{5} \times \frac{7}{\sqrt{5}}=7$

Area of the triangle ABC = 7 square units