Question:
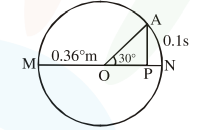
The point A moves with a uniform speed along the circumference of a circle of radius $0.36 \mathrm{~m}$ and covers $30^{\circ}$ in $0.1 \mathrm{~s}$. The perpendicular projection ' $\mathrm{P}$ ' from 'A' on the diameter $\mathrm{MN}$ represents the simple harmonic motion of ' $P$ '. The restoration force per unit mass when $P$ touches $M$ will be :
Correct Option: , 4
Solution:
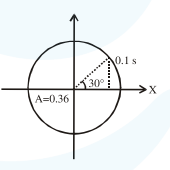
$30^{\circ} \rightarrow 0.1 \mathrm{~s}$
$360^{\circ} \rightarrow 1.2 \mathrm{~s}=\mathrm{T}$
$\omega=\frac{2 \pi}{T}=\frac{5 \pi}{3}$
At $\mathrm{M}, \mathrm{F}=\mathrm{m} \omega^{2} \mathrm{~A} \Rightarrow \frac{\mathrm{F}}{\mathrm{m}}=\omega^{2} \mathrm{~A}$
