The path of a train A is given by the equation 3x + 4y − 12 = 0

The given equation are $3 x+4 y-12=0$ and $6 x+8 y-48=0$.

In order to represent the above pair of linear equation graphically, we need

Two points on the line representing each equation. That is, we find two solutions

of each equation as given below:

We have,

$3 x+4 y-12=0$

Putting $y=0$, we get

$3 x+0-12=0$

$\Rightarrow x=4$

Putting $x=0$ we get

$0+4 y-12=0$

$\Rightarrow y=3$

Thus, two solution of equation $3 x+4 y-12=0$ are

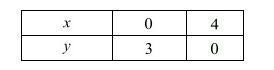
We have $6 x+8 y-48=0$

Putting $y=0$, we get

$6 x+0-48=0$

$\Rightarrow x=8$

Putting $x=0$ we get

$0+8 y-48=0$

$\Rightarrow y=6$

Thus, two solution of equation $6 x+8 y-48=0$ are

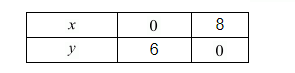
Now we plot the point $A(4,0)$ and $B(0,3)$ and draw a line passing through

These two points to get the graph o the line represented by equation(1)

       We also plot the points $C(8,0)$ and $D(0,6)$ and draw a line passing through

These two points to get the graph $\mathrm{O}$ the line represented by equation $(2)$

We observe that the line parallel and they do not intersect anywhere.