Question:
The number of students absent in a class were recorded every day for 120 days and the information is given in the following frequency table:
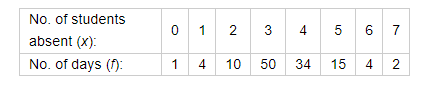
Find the mean number of students absent per day.
Solution:
Let the assume mean be $A=4$.
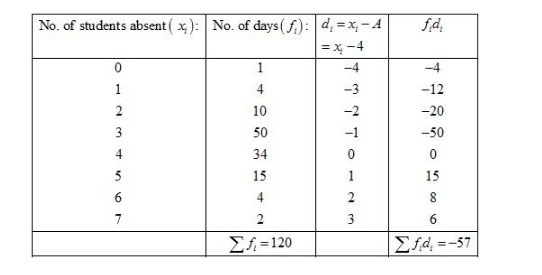
We know that mean, $\bar{X}=A+\frac{1}{N} \sum_{i=1}^{n} f_{i} d_{i}$
Now, we have $N=\sum f_{i}=120, \sum f_{i} d_{i}=-57$ and $A=4$.
Putting the values in the above formula,
$\bar{X}=A+\frac{1}{N} \sum_{i=1}^{n} f_{i} d_{i}$
$=4+\frac{1}{120} \times(-57)$
$=4-\frac{57}{120}$
$=4-0.475$
$=3.525$
$\approx 3.53$ (approximate)
Hence, the mean number of students absent per day is approximately 3.53.
