Question:
The number of real roots of the equation $e^{6 x}-e^{4 x}-2 e^{3 x}-12 e^{2 x}+e^{x}+1=0$ is :
Correct Option: 1
Solution:
$e^{6 x}-e^{4 x}-2 e^{3 x}-12 e^{2 x}+e^{x}+1=0$
$\Rightarrow\left(e^{3 x}-1\right)^{2}-e^{x}\left(e^{3 x}-1\right)=12 e^{2 x}$
$\left(e^{3 x}-1\right)^{2}\left(e^{x}-e^{-x}-e^{-2 x}\right)=12$
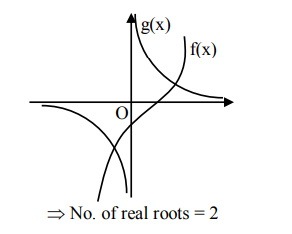
$\Rightarrow \underbrace{\mathrm{e}^{\mathrm{x}}-\mathrm{e}^{-\mathrm{x}}-\mathrm{e}^{-2 \mathrm{x}}}_{\text {increasing }(\operatorname{let} \mathrm{f}(\mathrm{x}))}=\underbrace{\frac{12}{\mathrm{e}^{3 \mathrm{x}}-1}}_{\text {decreasing }(\operatorname{let} g(\mathrm{x}))}$