Question:
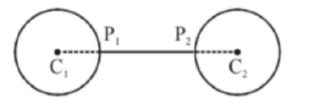
The minimum distance between any two points $P_{1}$ and $P_{2}$ while considering point $P_{1}$ on one circle and point $\mathrm{P}_{2}$ on the other circle for the given circles' equations
$x^{2}+y^{2}-10 x-10 y+41=0$
$x^{2}+y^{2}-24 x-10 y+160=0$
Solution:
Given $\mathrm{C}_{1}(5,5), \mathrm{r}_{1}=3$ and $\mathrm{C}_{2}(12,5), \mathrm{r}_{2}=3$
Now, $\mathrm{C}_{1} \mathrm{C}_{2}>\mathrm{r}_{1}+\mathrm{r}_{2}$
Thus, $\left(\mathrm{P}_{1} \mathrm{P}_{2}\right)_{\min }=7-6=1$