The median of the following data is 50.

Solution:

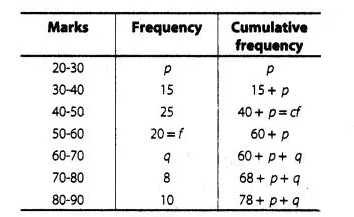
Given $N=90$

$\therefore$ $\frac{N}{2}=\frac{90}{2}=45$

which lies in the interval $50-60$.

Lower limit, $l=50, f=20, c f=40+p, h=10$

$\therefore$ Median $=l+\frac{\left(\frac{N}{2}-c f\right)}{f} \times h$

$=50+\frac{(45-40-\rho)}{20} \times 10$

$\Rightarrow$ $50=50+\left(\frac{5-p}{2}\right)$

$\Rightarrow$ $0=\frac{5-p}{2}$

$\therefore$ $p=5$

Also, $78+p+q=90$  [given]

$\Rightarrow \quad 78+5+q=90$

$\Rightarrow \quad q=90-83$

$\therefore \quad \quad q=7$