The mean and standard deviation of some data for the time taken to complete a test are calculated with the following results:
Number of observations $=25$, mean $=18.2$ seconds, standard deviation $=3.25$ seconds.
Further, another set of 15 observations $x_{1}, x_{2, \ldots,} x_{15}$, also in seconds, is now available and we have
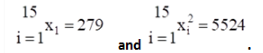
Calculate the standard derivation based on all 40 observations.
Given: Number of observations $=25$, mean $=18.2$ seconds, standard deviation = $3.25$ seconds. Another set of 15 observations $x_{1}, x_{2}, \ldots, x_{15}$, also in seconds,
is $\underset{i=1}{15} x_{1}=279$ and ${ }_{i=1}^{15} x_{i}^{2}=5524$
Now we have to find the standard derivation based on all 40 observations As per the given criteria,
In first set,
Number of observations, $n_{1}=25$
Mean, $\overline{x_{1}}=18.2$
And standard deviation, $\sigma_{1}=3.25$
And
In second set,
Number of observations, $n_{2}=15$

For the first set we have
$\overline{x_{1}}=18.2=\frac{\sum x_{i}}{25}$
$\sum x_{i}=25 \times 18.2=455$
Therefore the standard deviation becomes,
$\sigma_{1}^{2}=\frac{\sum x_{i}^{2}}{25}-(18.2)^{2}$
Substituting the values, we get
$(3.25)^{2}=\frac{\sum x_{i}^{2}}{25}-331.24$
$\Rightarrow 10.5625+331.24=\frac{\sum x_{i}^{2}}{25}$
On rearranging we get
$\Rightarrow \frac{\sum x_{i}^{2}}{25}=341.8025$
On cross multiplication we get
$\Rightarrow \sum x_{i}^{2}=25 \times 341.8025=8545.06$
For the combined standard deviation of the 40 observation, $n=40$
And
$\Rightarrow \sum x_{i}^{2}=8545.06+5524=14069.69$
$\Rightarrow \sum x_{i}=455+279=734$
Therefore the standard deviation can be written as,
$\sigma=\sqrt{\frac{\sum x_{i}^{2}}{n}-\left(\frac{\sum x_{i}}{n}\right)^{2}}$
Substituting the values, we get
Therefore the standard deviation can be written as,
$\sigma=\sqrt{\frac{14069.69}{40}-\left(\frac{734}{40}\right)^{2}}$
On simplifying we get
$\sigma=\sqrt{351.7265-(18.35)^{2}}$
$\sigma=\sqrt{351.7265-336.7225}$
$\sigma=\sqrt{15.004}$
$\sigma=3.87$
Hence the standard derivation based on all 40 observations is $3.87 .$
