The maximum volume (in cu. m ) of the right circular

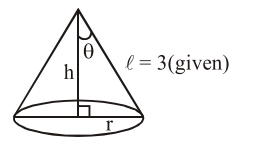
$\therefore \mathrm{h}=3 \cos \theta$

$r=3 \sin \theta$

Now,

$\mathrm{V}=\frac{1}{3} \pi \mathrm{r}^{2} \mathrm{~h}=\frac{\pi}{3}\left(9 \sin ^{2} \theta\right) \cdot(3 \cos \theta)$

$\therefore \quad \frac{\mathrm{dV}}{\mathrm{d} \theta}=0 \Rightarrow \sin \theta=\sqrt{\frac{2}{3}}$

Also, $\left.\frac{\mathrm{d}^{2} \mathrm{~V}}{\mathrm{~d} \theta^{2}}\right]_{\sin \theta-\sqrt{\frac{2}{3}}}=$ negative

$\Rightarrow$ Volume is maximum,

when $\sin \theta=\sqrt{\frac{2}{3}}$

$\therefore \quad \mathrm{V}_{\max }\left(\sin \theta=\sqrt{\frac{2}{3}}\right)=2 \sqrt{3} \pi$ (in cu. $\left.\mathrm{m}\right)$