The lowest integer which is greater than

Let $P=\left(1+\frac{1}{10^{100}}\right)^{10^{100}}$

Let $x=10^{100}$

$\Rightarrow P=\left(1+\frac{1}{x}\right)^{x}$

$\Rightarrow P=1+(x)\left(\frac{1}{x}\right)+\frac{(x)(x-1)}{\lfloor 2} \cdot \frac{1}{x^{2}}$

$+\frac{(x)(x-1)(x-2)}{\lfloor 3} \cdot \frac{1}{x^{3}}+\ldots$

(upto $10^{100}+1$ terms)

$\Rightarrow P=1+1+\left(\frac{1}{12}-\frac{1}{12 x^{2}}\right)+\left(\frac{1}{13}-\ldots\right)+\ldots$ so on

$\Rightarrow P=2+\left(\right.$ Positive value less then $\left.\frac{1}{\lfloor 2}+\frac{1}{\mid 3}+\frac{1}{4}+\ldots\right)$

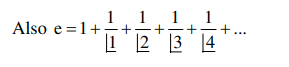
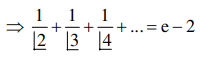
$\Rightarrow P=2+($ positive value less then $e-2)$

$\Rightarrow P \in(2,3)$

$\Rightarrow$ least integer value of $\mathrm{P}$ is 3