Question:
The locus of the centres of the circles, which touch the circle, $x^{2}+y^{2}=1$ externally, also touch the $\mathrm{y}$-axis and lie in the first quadrant, is :
Correct Option: , 4
Solution:
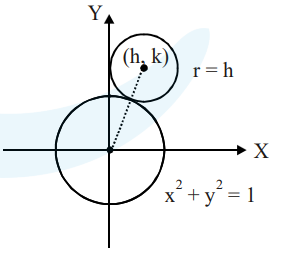
$\sqrt{\mathrm{h}^{2}+\mathrm{k}^{2}}=|\mathrm{h}|+1$
$\Rightarrow x^{2}+y^{2}=x^{2}+1+2 x$
$\Rightarrow y^{2}=1+2 x$
$\Rightarrow y=\sqrt{1+2 x} ; \quad x \geq 0$
