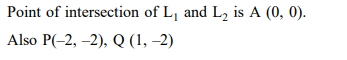Question:
The lines $\mathrm{L}_{1}: \mathrm{y}-\mathrm{x}=0$ and $\mathrm{L}_{2}: 2 \mathrm{x}+\mathrm{y}=0$ intersect the line $\mathrm{L}_{3}: \mathrm{y}+2=0$ at $\mathrm{P}$ and $\mathrm{Q}$ respectively. The bisector of the acute angle between $L_{1}$ and $L_{2}$ intersects $L_{3}$ at $R$.
Statement - 1 : The ratio PR : RQ equals $2 \sqrt{2}: \sqrt{5}$
Statement - 2 : In any triangle, bisector of an angle divides the triangle into two similar triangles.
Correct Option: 1
Solution: