Question:
The lines $x=$ ay $-1=z-2$ and $x=3 y-2=b z-2,(a b \neq 0)$ are coplanar, if :
Correct Option: 1
Solution:
$\frac{x+1}{a}=y=\frac{z-1}{a}$
$\frac{x+2}{3}=y=\frac{z}{3 / b}$
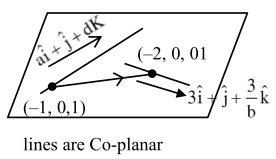
$\left|\begin{array}{ccc}\mathrm{a} & 1 & \mathrm{a} \\ 3 & 1 & \frac{3}{\mathrm{~b}} \\ -1 & 0 & -1\end{array}\right|=0 \Rightarrow-\left(\frac{3}{\mathrm{~b}}-\mathrm{a}\right)-1(\mathrm{a}-3)=0$
$a-\frac{3}{b}-a+3=0$
$b=1, a \in R-\{0\}$
