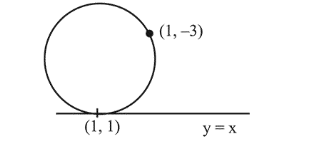
Question:
The line $x=y$ touches a circle at the point $(1,1)$. If the circle also passes through the point $(1,-3)$, then its radius is:
Correct Option: , 2
Solution:
Equation of circle which touches the line $y=x$ at $(1,1)$
is, $(x-1)^{2}+(y-1)^{2}+\lambda(y-x)=0$
This circle passes through $(1,-3)$
$\therefore 0+16+\lambda(-3-1)=0$
$\Rightarrow 16+\lambda(-4)=0 \Rightarrow \lambda=4$
Hence, equation of circle will be,
$(x-1)^{2}+(y-1)^{2}+4 y-4 x=0$
$\Rightarrow x^{2}+y^{2}-6 x+2 y+2=0$
$\therefore$ Radius $=\sqrt{9+1-2}=2 \sqrt{2}$
