The lengths of two parallel chords of a circle are 6 cm and 8 cm.

Solution:

Distance of smaller chord AB from centre of circle = 4 cm, OM = 4 cm

MB = AB/2 = 6/2 = 3 cm

In ΔOMB

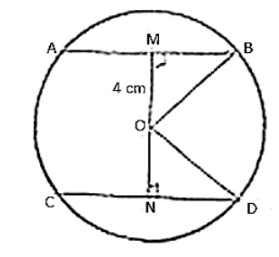
$\mathrm{OM}^{2}+\mathrm{MB}^{2}=\mathrm{OB}^{2}$

$4^{2}+9^{2}=\mathrm{OB}^{2}$

$16+9=\mathrm{OB}^{2}$

$O B=\sqrt{25}$

OB = 5 cm

In ΔOND

OD = OB = 5 cm [Radii of same circle]

ND = CD/2 = 8/2 = 4 cm

$O N^{2}+N D^{2}=O D^{2}$

$O N^{2}+4^{2}=5^{2}$

$O N^{2}=25-16$

$O N=\sqrt{9}$

ON = 3 cm

So, the distance of bigger chord from the circle is 3 cm.