The lengths of the diagonals of a rhombus are 24 cm and 10 cm.

(b) 13 cm

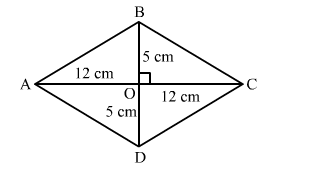
Let ABCD be the rhombus with diagonals AC and BD intersecting each other at O.
We have:
AC = 24 cm and BD = 10 cm
We know that diagonals of a rhombus bisect each other at right angles.
Therefore applying Pythagoras theorem in right-angled triangle AOB, we get:

$A B^{2}=A O^{2}+B O^{2}=12^{2}+5^{2}$

$=144+25=169$

$A B=\sqrt{169}=13$

Hence, the length of each side of the rhombus is 13 cm.