The length of the tangent drawn from a point 8 cm away form the centre of a circle of radius 6 cm is

Let us first put the given data in the form of a diagram.

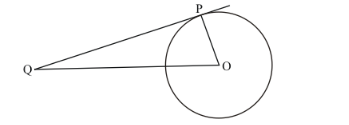
We know that the radius of a circle will always be perpendicular to the tangent at the point of contact. Therefore, OP is perpendicular to QP. We can now use Pythagoras theorem to find the length of QP.

$Q P^{2}=O Q^{2}-O P^{2}$

$Q P^{2}=8^{2}-6^{2}$

$Q P^{2}=64-36$

$Q P^{2}=28$

$Q P=\sqrt{28}$

$Q P=2 \sqrt{7}$

Therefore, the correct answer is option (b).