The length of the perpendicular

Let $P$ be the foot of perpendicular from point

$T(2,-1,4)$ on the given line. So $P$ can be assumed as

$P(10 \lambda-3,-7 \lambda+2, \lambda)$

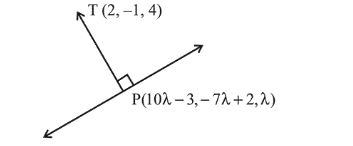
DR's of $T P$ is proportional to $10 \lambda-5,-7 \lambda+3, \lambda-4$

$\because \quad T P$ and given line are

perpendicular, so

$10(10 \lambda-5)-7(-7 \lambda+3)+1(\lambda-4)=0$

$\Rightarrow \lambda=\frac{1}{2}$

$\Rightarrow T P=\sqrt{(10 \lambda-5)^{2}+(-7 \lambda+3)^{2}+(\lambda-4)^{2}}$

$=\sqrt{0+\frac{1}{4}+\frac{49}{4}}=\sqrt{12.5}=3.54$

Hence, the length of perpendicular is greater than 3 but less than $4 .$