The length of the diagonal of a square is 24 cm. Find its area.

The diagonal of a square forms the hypotenuse of an isosceles right triangle. The other two sides are the sides of the square of length a cm.

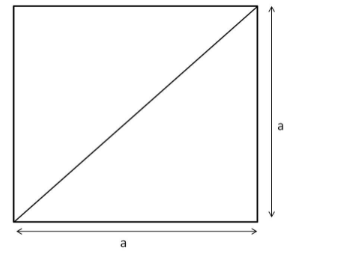
Using Pythagoras' theorem, we have:

Diagonal $^{2}=a^{2}+a^{2}=2 a^{2}$

$\Rightarrow$ Diagonal $=\sqrt{2} a$

Diagonal of the square $=\sqrt{2} a$

$\Rightarrow 24=\sqrt{2} a$

$\Rightarrow a=\frac{24}{\sqrt{2}}$

Area of the square $=\operatorname{Side}^{2}=\left(\frac{24}{\sqrt{2}}\right)^{2}=\frac{24 \times 24}{2}=288 \mathrm{~cm}^{2}$