Question:
The length of a square field is 0.5 hectare. The length of its diagonal is
(a) $150 \mathrm{~m}$
(b) $100 \sqrt{2}$
(c) 100 m
(d) $50 \sqrt{2} \mathrm{~m}$
Solution:
(c) 100 m
Disclaimer :- The length cannot be in hectare So we used is as area of the square.
Area of the square field $=0.5 \times 10000=5000 \mathrm{~m}^{2}$
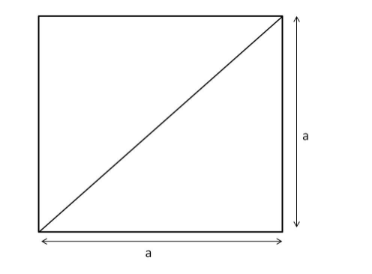
The diagonal divides the square into two isosceles right-angled triangles.
Using Pythagoras' theorem, we have:
Diagonal $^{2}=a^{2}+a^{2}=2 a^{2}$
Area of a square $=a^{2}$
$\therefore$ Diagonal $=\sqrt{2 \text { area }}=\sqrt{2 \times 5000}=\sqrt{10000}=100 \mathrm{~m}$
