The length of a potentiometer wire is $1200 \mathrm{~cm}$ and it carries a current of $60 \mathrm{~mA}$. For a cell of emf $5 \mathrm{~V}$ and internal resistance of $20 \Omega$, the null point on it is found to be at $1000 \mathrm{~cm}$. The resistance of whole wire is:
Correct Option: , 4
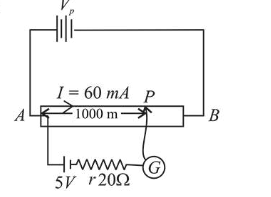
Let $R$ be the resistance of the whole wire Potential gradient for the potentiometer wire
$' A B^{\prime}=-\frac{d V}{d \ell}=\frac{I \times R}{\ell}=\left[\frac{60 \times R}{\ell_{A B}}\right] \mathrm{mv} / \mathrm{m}$
$V_{A P}=\left(\frac{d V}{d \ell_{A B}}\right) \ell_{A P}=\frac{60 \times R}{1200} \times 1000 \mathrm{mV}$
$\Rightarrow V_{A P}=50 \mathrm{R} m V$
Also, $V_{A P}=5 V($ for balance point at $P)$
$\therefore R=\frac{V_{A P}}{50 \times 10^{-3}}=\frac{5}{50 \times 10^{-3}}=100 \Omega$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.