The ionization constant of phenol is $1.0 \times 10^{-10}$. What is the concentration of phenolate ion in $0.05 \mathrm{M}$ solution of phenol? What will be its degree of ionization if the solution is also $0.01 \mathrm{M}$ in sodium phenolate?
Ionization of phenol:
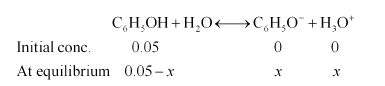
$K_{a \pi}=\frac{\left[\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{O}^{-}\right]\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}{\left[\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{OH}\right]}$
$K_{a}=\frac{x \times x}{0.05-x}$
As the value of the ionization constant is very less, $x$ will be very small. Thus, we can ignore $x$ in the denominator.
$\therefore x=\sqrt{1 \times 10^{-10} \times 0.05}$
$=\sqrt{5 \times 10^{-12}}$
$=2.2 \times 10^{-6} \mathrm{M}=\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]$
Since $\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\left[\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{O}^{-}\right]$
$\left[\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{O}^{-}\right]=2.2 \times 10^{-6} \mathrm{M}$
Now, let $\propto$ be the degree of ionization of phenol in the presence of $0.01 \mathrm{M} \mathrm{C}_{6} \mathrm{H}_{5} \mathrm{ONa}$.
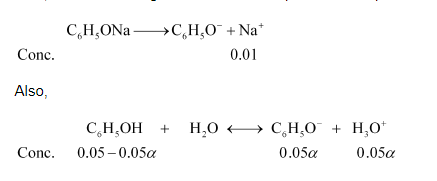
$\left[\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{OH}\right]=0.05-0.05 \alpha ; 0.05 \mathrm{M}$
$\left[\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{O}^{-}\right]=0.01+0.05 \alpha ; 0.01 \mathrm{M}$
$\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=0.05 \alpha$
$K_{o}=\frac{\left[\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{O}^{-}\right]\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}{\left[\mathrm{C}_{6} \mathrm{H}_{5} \mathrm{OH}\right]}$
$K_{a}=\frac{(0.01)(0.05 \alpha)}{0.05}$
$1.0 \times 10^{-10}=.01 \alpha$
$\alpha=1 \times 10^{-8}$
