The interior of a building is in the form of a right circular cylinder of diameter 4.2 m

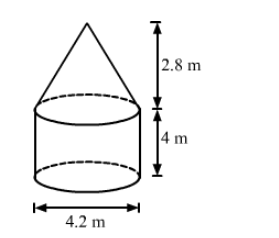
We have,

Radius of the cylinder $=$ Radius of the cone $=r=\frac{4.2}{2}=2.1 \mathrm{~m}$,

Height of the cylinder, $H=4 \mathrm{~m}$ and

Height of the cone, $h=2.8 \mathrm{~m}$

Also,

The slant height of the cone, $l=\sqrt{r^{2}+h^{2}}$

$=\sqrt{2.1^{2}+2.8^{2}}$

$=\sqrt{4.41+7.84}$

$=\sqrt{12.25}$

$=3.5 \mathrm{~m}$

Now,

The outer surface area of the building $=$ CSA of the cylinder $+$ CSA of the cone

$=2 \pi r H+\pi r l$

$=\pi r(2 H+l)$

$=\frac{22}{7} \times 2.1 \times(2 \times 4+3.5)$

$=6.6 \times 11.5$

$=75.9 \mathrm{~m}^{2}$

So, the outer surface area of the building is 75.9 m2.