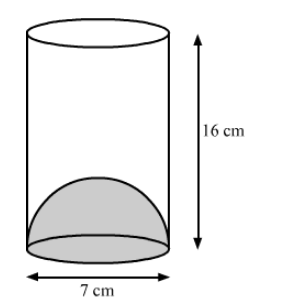
The inner diameter of a glass is 7 cm and it has a raised portion in the bottom in the shape of a hemisphere, as shown in the figure.

We have,

the height of the glass, $h=16 \mathrm{~cm}$ and

the base radius of cylinder $=$ the base radius of hemisphere, $r=\frac{7}{2} \mathrm{~cm}$

Now,

The apparent capacity of the glass = Volume of the cylinder

$=\pi r^{2} h$

$=\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2} \times 16$

$=616 \mathrm{~cm}^{3}$

Also,

The actual capacity of the glass $=$ Volume of cylinder $-$ Volume of hemisphere

$=616-\frac{2}{3} \pi r^{3}$

$=616-\frac{2}{3} \times \frac{22}{7} \times \frac{7}{2} \times \frac{7}{2} \times \frac{7}{2}$

$=616-\frac{539}{6}$

$=\frac{3157}{6} \mathrm{~cm}^{3}$

$\approx 526.17 \mathrm{~cm}^{3}$