The inner and outer radii of a hollow cylinder are 15 cm and 20 cm,

Inner radius of hollow cylinder r1 = 15 cm

Outer radius of hollow cylinder r2 = 20 cm

The volume of hollow cylinder $=\pi\left(r_{2}^{2}-r_{1}^{2}\right) h$

Since,

The hollow cylinder is melted and recast into a solid cylinder of same height.

Let r be the radius of solid cylinder.

Therefore,

The volume of solid cylinder = volume of hollow cylinder.

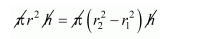
$r^{2}=\left(20^{2}-15^{2}\right)$

$r^{2}=35 \times 5$

$r=13.2 \mathrm{~cm}$

Hence, the radius of solid cylinder is $13.2 \mathrm{~cm}$.