The image of an object placed at a point A before a plane mirror LM is seen at the point B by an observer at D,

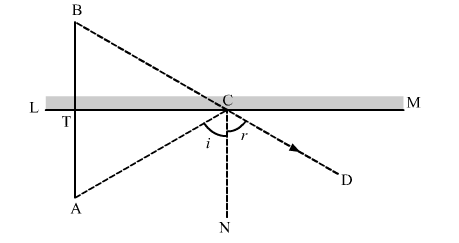
Given: An object is placed at a point A, the image of the object is seen at the point B, an observer is at point D, and LM is a plane mirror.

To Prove: The image is as far behind the mirror as the object is in front of the mirror, i.e. BT = AT.

Proof:

$\because L M$ is a plane mirror

$\therefore i=r$      (Angle of incidence is always equal to angle of reflection)    .....(1)

Also, $A B \| C N$     (Both AB and CN are perpendicular to LM)

$\Rightarrow \angle T A C=\angle A C N=i$    (Alternate interior angles)      .....(2)

And, $\angle C B T=\angle N C D=r$              (Corresponding angles)         .....(3)

From (1), (2) and (3), we get

$\angle T A C=\angle C B T$                         ...............(4)

Now,

In $\Delta T A C$ and $\Delta C B T$,

$\angle T A C=\angle C B T \quad[$ From $(4)]$

$\angle A T C=\angle B T C=90^{\circ}$

$C T=C T \quad$ (Common side)

$\therefore$ By AAS congruence criteria,

$\Delta T A C \cong \Delta C B T$

Hence, AT = BT    (CPCT)